Игра Маленькое Королевство: Гастон лабиринт
Предыдущая игра
Следующая игра
Управление в игре
Стрелочки-курсорыпередвигаться.
Описание: как играть
Бесплатная онлайн игра
Маленькое Королевство: Гастон лабиринт / Little Kingdom Gaston’s A-Maze-ing Game.Как запустить флеш игру (How to run flash game)
Скачайте портативный браузер Mozilla Firefox, чтобы запускать флеш игры онлайн. Он не требует особой установки: просто разархивируйте его в любое место, используя архиватор, поддерживающий 7-Zip архивы.
Для того, чтобы запустить сам браузер, нужно зайти в разархивированную папку и запустить ярлык под названием FirefoxPortable.exe (первый запуск может быть немного медленным, если у вас слабый Интернет).
Мы рады Вас приветствовать в маленьком царстве Гастона. Мы о нем ранее немного упоминали, но повторим еще: это маленькая божья коровка, которая имеет собачьи повадки, потом что иногда лает как пес и любит, чтобы его почесывали за ушком. Это любимец Холли и Бена, который живет в своей норке. Вы должны помогать этому насекомому собрать побольше разных вкусностей, которые накопились в его лабиринте. Он никак не может понять, как эльфы и феи могут разбрасывать такими лакомствами как: недоеденными шоколадками, шкурками от помидоров, яблочными огрызками. Ему этого, видимо, никогда не понять, так как для него это любимая еда. Вы будете сопровождать его, чтобы он смог собрать побольше еды, а потом нашел выход и побыстрее добрался к своей норке. Здесь есть два уровня сложности: легкий и и сложный. Сложный отличается тем, что на пути будут встречаться опасные муравьи, а время на передвижение будет ограничено, потому нужно спешить. Дерзайте!
Избранные игры Мои игры: 0
Добавить
в избранные
Если игра понравилась — добавь её в избранное!
чтобы не потерять
01
galvana
1121
02
s245s
370
03
zurogieva
140
04
PORIDZH
134
05
скиздо
122
06
Bambi the Gamer
117
07
fhjwsefse46556
111
08
Advlad
93
Misukee
90
10
скиздо
81
- Игры онлайн бесплатно для девочек и мальчиков —
fog-game.
ru © 2022 - Обратная связь
- Вопросы и ответы
- Правообладателям
Но я два… нет, три раза видел, как он прибор вытаскивал и чего-то делал. Как будто топограф местность изучает… И еще в мешке много других вещей есть. Нам Мурад рассказывал, он всегда таскает барахло Кара-Шайтана… «Счетчик радиации, наверное, — мысленно предположил Сергей. — Урановые руды ищет? Или, может быть, проверяет слухи, будто в этих горах остались с советских времен атомные боеприпасы…» Отпустив пленного, Гастон сказал: — Командор, надо убивать этот Кара-Шайтан. Серж, ви дольжен делать этот петит операсьон. — Сейчас у нас другие задачи, нет времени на твои «маленькие операции», — отрезал подполковник. — Быстрее закругляйся здесь и полезай в грузовик. С бандой Хандруева было покончено. Сводная рота спецназа, погрузившись в трофейные машины, тряслась по плохой дороге. Утомленный нелегким днем, Сергей привалился к борту кузова. Гастон подобрался к нему, сел рядом и снова стал уговаривать командира повернуть роту на юг, прочесать горы от Чограй-Юрта до истоков Айгура и уничтожить банду таинственного Кара-Шайтана. Он даже намекнул, что на этом деле можно заработать неплохие бабки. Гастон явно имел какой-то интерес, и Сергей, как ему казалось, догадывался, в чем тут дело. Подполковник предполагал, что француз был агентом какой-то зарубежной спецслужбы, а Кара-Шайтан состоял в конкурирующем ведомстве другого государства… В любом случае не имело смысла гоняться по горам за крохотным отрядом боевиков, когда назревали большие неприятности в Грозном. Сейчас подполковника гораздо больше интересовала личность самого Гастона, поэтому Сергей осведомился: — Ты — хороший солдат, старик. — Меня долго учили, — по обыкновению, уклончиво ответил иностранец. — И где ты воевал — Африка, Вьетнам, Афганистан? — Луандьё… далеко отсюда. — Обгорелая маска по-прежнему не выражала эмоций. — И русскому языку тоже научили давно и далеко. — Сергей не собирался отступать. — Нет, командор, этому я научился поближе и совсем недавно. — Гастон отвел взгляд. — Ты тоже хороший солдат, командор. Но ты много не понимать… Здесь появляться террибле… страшный опасность для всех. Я один не могу победить, ты один тоже не можешь победить. Вместе надо. Но если ты не хотеть помогать, я буду пойти один. — Никуда ты без моего приказа не пойдешь, даже в сортир! — повысил голос Сергей. — Будешь играть в свои шпионские игры, когда кончится срок контракта с «Финистом». Вместо ответа мсье Машен похлопал его по плечу и перебрался на другой конец кузова. У подполковника совершенно не было настроения заниматься неврозами закордонного гостя. Он снова переживал неприятные обстоятельства сегодняшнего боя. Вскоре после полудня, когда августовский зной становится совсем невыносимым, «финисты» прибыли в Ханкалу. Здесь, на авиабазе, расположенной неподалеку от Грозного, обосновался штаб Объединенной группировки войск министерств обороны и внутренних дел. Подполковник приказал Рубцову организовать для личного состава баню, кормежку и отдых, а также сдать куда положено пленных, захваченные документы и часть трофейной техники. В штабе Сергей потребовал встречи с командующим. Оказалось, что тот недавно отбыл в отпуск и можно поговорить только с заместителем командующего генерал-лейтенантом Куликовским. «Надо же, здесь Кирилл за главного», — обрадовался Сергей. Они познакомились лет семь назад, когда полк внутренних войск полковника Куликовского был переброшен в охваченную массовыми беспорядками республиканскую столицу. Там же, на окраине огромного южного города, дислоцировался «Кальмар» — дивизион подводных диверсантов, которым командовал майор Каростин. Тогда им удалось совместными усилиями перемолотить орду погромщиков, за что оба офицера понесли суровые наказания: Кирилла сослали на должность замначальника колонии усиленного режима в забайкальскую глухомань, а Сергея и вовсе выгнали из армии. — Вы получили мое предупреждение о намеченном штурме Грозного? — первым делом осведомился командир «финиста». — И твое предупреждение получили, и по линии военной контрразведки получили, и чеченское МВД о том же сообщает, — успокоил его Куликовский. — Не беспокойся, мы готовы отразить любую атаку. Они обсудили боевую обстановку, и Сергей попросил передать в Москву, чтобы сюда перебросили остальные подразделения «Финиста»: в такой напряженной обстановке следовало бы стянуть в столицу воюющей республики лучшие части спецназа. Кирилл заверил, что обязательно передаст его рапорт по инстанции. — Значит, встретим их как положено, — сказал Сергей. — Пойду-ка я немного покемарю, а вечером начнем зачистку выявленных баз противника в городе. Он уже собирался уходить, но вдруг вспомнил утренние события и осведомился, что известно штабу о банде некоего Кара-Шайтана. — Есть такой полевой командир из числа безобидных, — ответил генерал. — От активных боевых действий с нашими войсками старательно уклоняется, поэтому и мы не трогаем его отряд. В общем, он нам не досаждает. Личный состав «Финиста» бездельничал до самого вечера, а потом из Москвы поступил приказ немедленно возвращаться на место постоянного базирования части — спецназ срочно понадобился для других дел. Транспортный Ил-96 уходил через час с небольшим, так что грузиться пришлось в обстановке общего аврала. Только в полете выяснилось, что на борту отсутствует Гастон Машен. Пропажа иностранца попахивала международным скандалом, но возвращать самолет на чеченский аэродром было невозможно, поэтому Сергей бросился к командиру экипажа и отправил тревожные радиограммы в Москву и Ханкалу. Утром следующего дня, когда он был уже в штабе полка, поступили ответы. Из Чечни сообщили, что на территории авиабазы «Ханкала» Машена обнаружить не удалось. Еще интереснее было другое: МИД Российской Федерации, равно как французское посольство, единодушно заверял, что гражданин Франции по имени Гастон Машен за последние три года на территорию России не въезжал. А на следующий день стало не до исчезнувшего француза: крупные силы чеченских формирований нанесли согласованный удар по основным объектам Грозного. Глава 2 ДАВНИЙ ПРИЯТЕЛЬ Аркадий Турин познакомился с Атиллой Бархановым в конце восьмидесятых годов на XVI Всесоюзной конференции по релятивистской астрофизике — так назывался раздел теоретической физики, изучавший происхождение и развитие Вселенной. Оба они, только-только защитив кандидатские диссертации, были полны идей, энтузиазма и иллюзий. Потом сверхдержава погрузилась в пучину хаоса, и люди интеллектуального труда внезапно стали никому не нужны. Сам Аркадий до прошлого лета был озабочен лишь одним — как бы прокормить семью. В конце концов он занялся подводным поиском антиквариата и нашел-таки удачу. Атилле пришлось похуже: властям его республики очень не нравилось, что доцент местного университета стал активистом Интерфронта и выступает против этнических чисток, искоренения русскоязычных секторов в высшей и средней школе, а также прочих проявлений местного расизма. |
Пользуясь свободными минутками, «финисты» распаковали пластиковые коробки экспериментального солдатского пайка ИРП-1 и с аппетитом рубали сосисочный фарш, перловку с мясом, галеты и тушенку, закусывая обед сладким изюмом и запивая эти радости жизни фруктовыми соками.
Где научился воевать?
Пули не раз свистели в угрожающей близости, а когда он брал Удава, этот бугай успел ударить подполковника кинжалом. Конечно, все обошлось — клинок, не причинив вреда, скользнул по титановым пластинам нагрудного панциря, но такой факт вообще не имел права на существование, поскольку роботы Лабиринта обязаны были защищать силовыми полями всех Посвященных. Однако энергетические барьеры не действуют вот уже который месяц, — стало быть, в Лабиринте случилось что-то чрезвычайное. Это серьезно беспокоило Сергея: неожиданный отказ инопланетной техники мог оказаться куда опаснее, чем любые земные войны, политические интриги или происки враждебных разведок.
Капитан правильно понял командирское «часть»: самая ценная добыча, вроде спутниковых раций, останется в распоряжении «Финиста».
— Я радировал в штаб с марша.
С такими, как он, всегда можно договориться по-хорошему… Ну, ступай. Я распоряжусь, чтобы тыловики позаботились о твоих людях.
Были и звонки с угрозами, и другие неприятности. Под нажимом администрации жизнь семьи Бархановых быстро сделалась невыносимой, так что пришлось второпях распродавать имущество и перебираться в Подмосковье. Сейчас Атилла втридорога снимал комнатушку в Мытищах, где ютился с женой и двумя маленькими детьми.Количество путей прохождения
Под возвращающимся [ возвратным ] лабиринтом я подразумеваю такой лабиринт, что в каждом узле его пути есть четное количество аллей.
Узлы, в которых имеется более двух переулков, будем называть узлами лабиринта.
Я буду различать по имени петля [ тупик ] каждый переулок, концы которого находятся на одном перекрестке.
{50}
Теорема о петле.
Если в повторно входном лабиринте удалить петлю, количество различных ходов сокращенного лабиринта,
умножается на количество его переулков, заканчивающихся на перекрестке с удаленной петлей,
равно количеству различных обходов исходного лабиринта.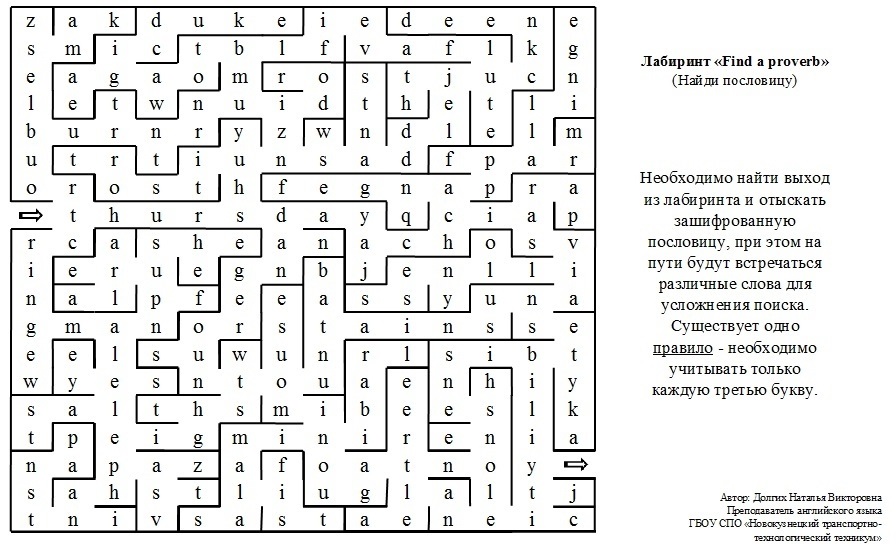
Обозначим через N количество различных ходов сокращенного лабиринта, а через 2 n количество его переулков заканчивающийся на стыке удаленной петли.
Я говорю, что количество различных ходов исходного лабиринта равно N ×2 n [14].
В самом деле, рассмотрим любой из N различных проходов сокращенного лабиринта.
В этом обходе мы пройдем n раз через перекресток, где была удалена петля, и на любом из них переходы, мы можем прервать прогулку, подойдя к этому перекрестку, сделать круг по этой петле, которая можно сделать в двух разных направлениях, и, вернувшись к развилке, закончить прогулку, которую мы начали.
Отсюда следует, что каждая из N прогулок редуцированного лабиринта обеспечит 2 n различных прогулок. оригинального лабиринта.
Таким образом, N проходов уменьшенного лабиринта дадут N × 2 n проходов.
оригинальный лабиринт.
Понятно, что эти N × 2 n проходов исходного лабиринта все разные, и что нет других способов пройти оригинальный лабиринт за одну прогулку.
Таким образом, теорема доказана.
Следствие.
Если на перекрестке 2( n + k ) переулков, из которых 2 k принадлежат k петлям, число различных ходов рассматриваемого лабиринта равно произведению n ( n +1)( n +2)…..( n + k −1)2 k по количеству различных ходов сокращенного лабиринта получается удалением к петель из рассматриваемого лабиринта.
В самом деле, добавление каждой из этих k петель по очереди к сокращенному лабиринту равносильно умножению количество различных прогулок на 2 n , 2( n +1), 2( n +2),….2( n + k −1).
Мы увидим, что теорема о петлях позволяет исключить петли из рассматриваемого лабиринта и уменьшить
подсчет количества различных ходов для случая, когда в лабиринте больше нет петель.
{51}
Теорема.
Для заданного лабиринта с возвратным входом без петель, состоящего из k соединений, если мы обозначим через 2 n количество переулков, заканчивающихся на одном из его перекрестков N, затем количество различных проходов рассматриваемого лабиринта равно сумме количества различных прогулок 1×3×5×7….. (2
Эти 1×3×5×7….. (2 n −1) новые лабиринты получаются путем группировки попарно, всеми возможными способами 2 n переулков, заканчивающихся на перекрестке N, а затем заменяя в каждой из этих групп каждую пару переулков новым переулком, соединяющим два перекрестка в конце этих переулков, или, в особом случае где обе аллеи пары заканчиваются на одном и том же перекрестке петлей, проходящей через этот перекресток.
Сгруппируем 2 n переулков развязки N в пары переулков всеми возможными способами.
Таким образом, мы получаем (2 n −1)(2 n −3)….. 5×3×1 различных группировок.
С каждой из этих групп свяжем все ходы рассматриваемого лабиринта, в которых, при каждом проезде перекрестка N, переулке, ведущем в него, и переулке, ведущем от него принадлежат одной и той же паре этой группы.
Легко видеть, что искомое число прогулок будет равно сумме чисел различных прогулки, соответствующие каждой группе, способом, который мы только что указали.
Допустим, что рассмотрим прогулки одной из этих групп и исследуем пары аллей. которые его составляют.
В каждой из этих n пар два переулка, рассматриваемые как выходы из перекрестка N, ведут либо к двум к разным перекресткам A, B или к одному и тому же перекрестку C.
В первом случае мы, очевидно, можем заменить два переулка NA и NB новым переулком AB, соединяющим перекрестки A и B,
поскольку это равносильно замене ходов ANB или BNA эквивалентными ходами AB или BA.
Во втором случае также ясно, что две аллеи, соединяющие перекрестки N и C, можно заменить петлей, проходящей через соединение C.
Таким образом, теорема полностью доказана.
Когда мы применим к новым лабиринтам тот же метод устранения петель и уменьшения числа переходов, мы {52} необходимо последовательными сокращениями дойти до того, что нам остается рассматривать только лабиринты без петель и содержащий только два соединения, и тогда проблема может быть решена.
В самом деле, очень легко показать, что число различных обходов лабиринта, содержащего только два перекрестка 2 n переулков равно 2(2 n −1)(2 n −2)4×3×2×1, если учитывать направление движения.
Примечание . — Лабиринт, имеющий только две нечетные вершины, можно пройти и целиком. одной прогулкой, проходящей только один раз через каждую аллею.
Легко видеть, что число различных обходов этого лабиринта такое же, как и для
лабиринт с повторным входом, полученный добавлением новой аллеи, соединяющей две нечетные вершины.
Видеть пластины I и II для применения метода расчета количества различных прогулок возвращающегося лабиринта, аллеи которого образуют стороны и диагонали семиугольника.
Пояснения к табличкам I и II.
Круги представляют собой соединения лабиринта.
Прямые линии, соединяющие два круга, представляют собой аллеи лабиринта, соединяющие два перекрестка.
Петли, то есть аллеи, концы которых находятся на одном перекрестке, показаны в виде равностороннего треугольника с вершиной на окружности, соответствующей этому соединению.
Идентификационная буква на каждой диаграмме используется в расчетах для обозначения количества проходов, соответствующих к этой диаграмме, после удаления любых треугольников (петель), которые могут быть на ней.
Все диаграммы, имеющие одинаковую форму, после такой редукции естественно обозначаются одной и той же буквой.
Отдельное число, помещенное рядом с каждой диаграммой, показывает, во сколько раз число прохождений полного
схему надо считать.
Рядом с каждой диаграммой помещен расчет числа, которое должно умножать количество прогулок редуцированная диаграмма в силу теоремы о петле.
Если идентификационная буква каждой диаграммы обозначает количество обходов, соответствующих сокращенной диаграмме, имеем следующую таблицу:
| Х | = | 15ч | Т 1 | = | 6D 1 + 144D 2 | |
| H | = | 8P 1 + 4P 2 + 8P 3 + 4P 4 | Т 2 | = | 2D 1 + 16D 2 | |
| Т 3 | = | 12D 2 | ||||
| П 1 | = | 6Q 1 + 4Q 2 + 16Q 3 + 16Q 4 | Т 4 | = | 2D 2 + 4D 3 | |
| P 2 | = | 8Q 1 + 16Q 3 + 2Q 5 + 16Q 6 | Т 5 | = | D 1 | |
| P 3 | = | 2Q 1 + Q 2 | ||||
| П 4 | = | 2Q 1 + Q 5 | Д 1 | = | 240 | |
| Д 2 | = | 12 | ||||
| Q 1 | = | 6T 1 + 24T 2 + 48T 3 | Д 3 | = | 2 | |
| Q 2 | = | 8 зуб. 1 + 24 зуб. 2 + 64Т 4 |
||||
| Q 3 | = | 2T 1 + 4T 2 | ||||
| Q 4 | = | 2T 2 + 4T 3 | ||||
| Q 5 | = | 48T 2 + 24T 5 | ||||
| Q 6 | = | 2Т 2 + 2Т 5 |
{53} Проведя расчеты, приведенные в этой таблице, находим, что искомое число прогулок X равно 129 976 320 [15].
Важное замечание . – Две диаграммы имеют одинаковое количество обходов, если их можно привести в соответствие,
перекресток за перекрестком таким образом, чтобы количество переулков, соединяющих любые два перекрестка на одной из диаграмм
равно количеству переулков, соединяющих соответствующие перекрестки на другой диаграмме.
Использование этой почти интуитивной теоремы значительно сокращает трудозатраты, позволяя одно и то же представление для диаграмм, которые возникают в разных формах.
Таким образом, все шестиугольники могут быть представлены одной и той же диаграммой H.
Чем заняться в архивах округа Гастон
Избранные истории
Винокурня, которую обязательно нужно увидеть
Журнал «Пункт назначения»
ВинокурняMuddy River Distillery гордится тем, что использует лучшие ингредиенты, рецепты ручной работы и перегонные кубы, изготовленные по индивидуальному заказу, для производства всех семи нынешних сортов рома. […]
Избранные истории
Наслаждайтесь аутентичным опытом гребли на реке в округе Гастон
Журнал «Пункт назначения»
Если вы ищете уникальное приключение на свежем воздухе, вы не ошибетесь, исследуя реку Катоба или ее Саут-Форк. […]
Избранные истории
Пусть The Gaston County ‘Cue Trail станет вашим проводником к хорошей еде
Журнал «Пункт назначения»
Являетесь ли вы поклонником или просто хотите попробовать что-то новое, загляните в «Cue Trail» округа Гастон.
У нас есть уникальные и исторические традиции в культуре барбекю, а также широкий выбор развлечений, которые вы можете попробовать. Пусть тропа округа Гастон станет вашим проводником. […]
Избранные истории
Добро пожаловать, искатели острых ощущений
Журнал «Пункт назначения»
Мы приносим удовольствие! Независимо от того, предпочитаете ли вы активный отдых или предпочитаете оставаться дома, у вас есть две отличные возможности провести захватывающий уик-энд в округе Гастон. […]
Избранные истории
Сохранение воды создает уникальные впечатления для путешественников
Журнал «Пункт назначения»
Река Катоба широко считается «Самой трудолюбивой рекой в Америке», потому что на милю река Катоба вырабатывает больше электроэнергии, чем любая другая река в Соединенных Штатах. […]
Избранные истории
3 захватывающих отдыха на выходных этой весной в округе Гастон
Журнал «Пункт назначения»
Встретьтесь с нами в округе Гастон на этих трех великих событиях; Приключенческая гонка и открытие эллинга в Макаденвилле, Tuck Fest в Национальном центре Уайтуотер США и чемпионат мира Red Bull UCI Pump Track с Bike Fest в парке Джорджа Постона.
